1941. Предок

Напишите программу, которая для двух заданных вершин дерева определяет, является ли одна из них предком другой.

Вход. Первая строка содержит количество вершин в дереве n (1 ≤ n ≤ 10⁵).

Во второй строке расположены n целых чисел, где i-е число обозначает номер непосредственного родителя вершины с номером i. Если значение равно нулю, то вершина является корнем дерева.

Третья строка содержит количество запросов m (1 ≤ m ≤ 10⁵). Каждая из следующих m строк содержит два различных целых числа a и b (1 ≤ a, b ≤ n), задающих очередной запрос.

Выход. Для каждого из m запросов выведите в отдельной строке число 1, если вершина a является предком вершины b, и 0 в противном случае.

Пример входа	Пример выхода
6 0 1 1 2 3 3 5 4 1 1 4 3 6 2 6 6 5	0 1 1 0 0

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Дерево будем представлять в виде ориентированного графа, в котором рёбра направлены от предков к потомкам (для экономии памяти).

Выполним на этом графе поиск в глубину (DFS) и для каждой вершины v назначим метки:

· d[v] – время входа (когда DFS впервые посещает вершину).

· f[v] – время выхода (когда DFS завершает обработку вершины).

Вершина a является предком вершины b, если выполняется неравенство:

d[a] < d[b] < f[b] < f[a]

Это означает, что интервал [d[b]; f[b]] полностью содержаться в интервале [d[a]; f[a]]. Так как для любой вершины b всегда выполняется неравенство d[b] < f[b], для проверки принадлежности вершины a к числу предков вершины b достаточно проверить два условия:

d[a] < d[b] и f[b] < f[a]

Пример

Граф, приведенный в примере, с расстановкой меток выглядит следующим образом:

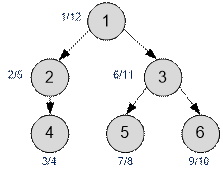
Например, вершина 1 является предком вершины 5, так как выполняются условия:

d[1] < d[5] и f[5] < f[1]

Действительно, интервал [7; 8] полностью содержится в интервале [1; 12].

Реализация алгоритма

Так как число вершин в графе может быть большим, будем хранить его в виде списка смежности g.

Для отслеживания уже посещённых вершин используем массив used.

Метки времени входа и выхода для каждой вершины будем сохранять в массивах d и f.

vector<vector<int> > g;

vector<int> used, d, f;

Функция dfs выполняет поиск в глубину, начиная из вершины v. Расставляем метки d[v] и f[v].

void dfs(int v)

{

used[v] = 1;

d[v] = time++;

for (int to : g[v])

if (!used[to]) dfs(to);

f[v] = time++;

}

Функция is_Parent возвращает 1, если вершина a является предком вершины b, и 0 в противном случае. Для этого проверяется включение отрезка [d[b]; f[b]] в отрезок [d[a]; f[a]], что эквивалентно выполнению двух неравенств:

d[a] < d[b] и f[b] < f[a]

int is_Parent(int a, int b)

{

return (d[a] < d[b]) && (f[b] < f[a]);

}

Основная часть программы. Читаем количество вершин графа n.

scanf("%d",&n);

Инициализируем массивы.

g.resize(n+1); used.resize(n+1);

d.resize(n+1); f.resize(n+1);

Читаем входной граф. Если вершина a является родителем вершины i, добавляем в граф ориентированное ребро (a, i) (для экономии памяти используем представление в виде ориентированного графа). Вершины графа нумеруются числами от 1 до n. Если a = 0, то вершина i является корнем дерева, и в этом случае ребро не добавляется. В переменной root находим номер вершины, являющейся корнем.

for(i = 1; i <= n; i++)

{

scanf("%d",&a);

if(!a) root = i; else g[a].push_back(i);

}

Запускаем поиск в глубину из корня root.

dfs(root);

Читаем запросы и выводим ответ на каждый из них за константное время.

scanf("%d",&m);

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

printf("%d\n",is_Parent(a,b));

}